

2004) of the behavior, and no unified theory on the physically based functional description has been found (Cleri 2005). Therefore, it is virtually impossible to develop a complete understanding (Chinh et al. This has been actively studied for decades. 2006 Turteltaub and Suiker 2005 Beese and Mohr 2012 Iwamoto and Tsuta 2000). 1995 Miller and McDowell 1996 Papatriantafillou et al. 1992 Bhattacharyya and Weng 1994 Diani et al. For austenitic steels and TRIP steels, the microstructural phase transformation from austenite to martensite also has a great effect on the plastic deformation. At the microscale, this aspect of plastic deformation is intrinsically coupled with all other aspects of plastic deformation such as development of preferred lattice orientations, formation of sub-grains, and formation of local shear bands (Wilson 1974). Additionally, it should be noted that the strain hardening behavior involves a complex interaction among various factors. Although excellent agreement has been provided for specific materials, the formulas have difficulty being adopted for other materials. 2015), TRIP steels (Tomita and Iwamoto 1995), high strength steels (Gardner and Ashraf 2006) and pipeline steels (Hertelé et al. Many formulas were designed to describe the full-range hardening and some material-specific formulas have been proposed for stainless steels (Rasmussen 2003 Gardner and Nethercot 2004a, b Abdella 2006 Quach et al. 2000 Tomita and Okabayashi 1985 Atkinson 1979 Kalidindi 1998 Saha et al.
#Engineering stress vs true stress pdf full#
However, this formula is inherently deficient to describe the strain hardening behavior of steels in the full range.ĭistinct stages strain hardening behavior has been observed in various types of steels (Jha et al.
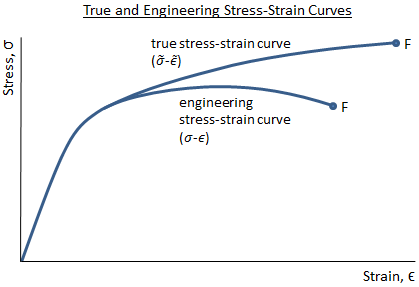
For this purpose, the Ramberg–Osgood formula (Ramberg and Osgood 1943) has been used widely for steels in various engineering fields. Therefore, some forms of analysis are normally to describe the strain hardening behavior of steels. The stages of polycrystalline steels are much less evident than those of the single crystal (Reedhill et al. 2004), typically three stages, labeled Stage I, Stage II and Stage III (Kuhlmann-Wilsdorf 1985). It is now well established that the hardening rate of crystals may be divided into various distinct stages (Nabarro et al. Typically, the strain hardening rate can be calculated numerically from the curves and plotted against strain (or stress). Strain hardening response of materials is usually characterized indirectly by the true stress–strain curves obtained from tensile tests.

The description of strain hardening behavior of materials using mathematical expression has been the subject of numerous investigations for many years. Finally, the proposed formula is considered to have wide suitability and high accuracy for all the steels tested. Furthermore, other formulas such as Ludwigson formula, Gardner formula, UGent formula are also applied for comparison. Excellent agreements with the test data are observed for all the steels tested. The parameters of the formula can be obtained directly and easily through linear regression analysis. The proposed formula can describe such behavior accurately in the full range using a single expression. Test results of all the six types of steels show a three-stage strain hardening behavior. For this purpose, a new formula is developed based on the well-known Ramberg–Osgood formula to describe the full range strain hardening behavior of steels. However, most of those formulas failed to describe accurately the strain hardening behavior of steels in the full range which shows various distinct stages. Various formulas have been developed to characterize stress strain curves of steels. Mathematical expression describing plastic behavior of steels allows the execution of parametric studies for many purposes.


 0 kommentar(er)
0 kommentar(er)
